线性回归原理

如图所示，这是一组二维的数据，我们先想想如何通过一条直线较好的拟合这些散点了？直白的说：尽量让拟合的直线穿过这些散点（这些点离拟合直线很近）。

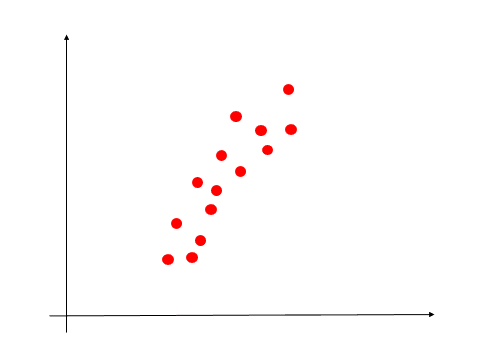
目标函数（成本函数）

要使这些点离拟合直线很近，我们需要用数学公式来表示：

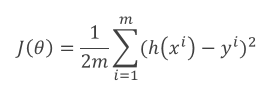
梯度下降法

之前在讲解回归时，是通过求导获取最小值，但必须满足数据可逆，这里通常情况下使用梯度下降法，也就是按着斜率方向偏移。详细可看这篇文章（）。

tips：这篇文章讲解了梯度上升法，梯度下降法类似。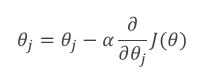

实战——房价预测

数据导入

该数据使用sklearn自带的数据集，通过sklearn.datasets导入我们的boston房价数据集。

from sklearn.datasets import load_bostonboston = load_boston()

通过DESCR属性可以查看数据集的详细情况，这里数据有14列，前13列为特征数据，最后一列为标签数据。

print(boston.DESCR)

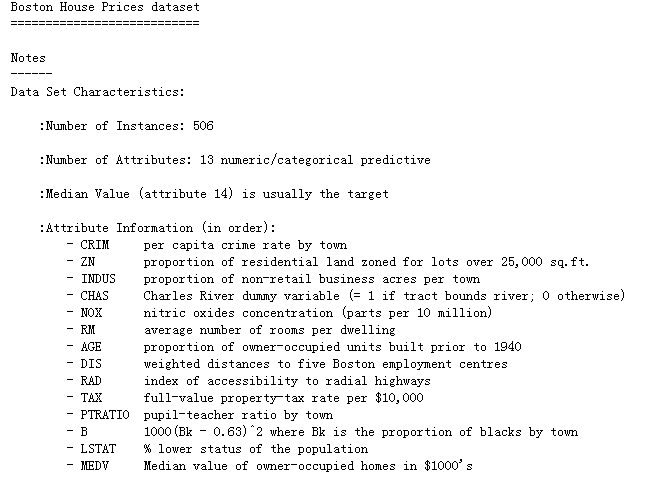
boston的data和target分别存储了特征和标签：

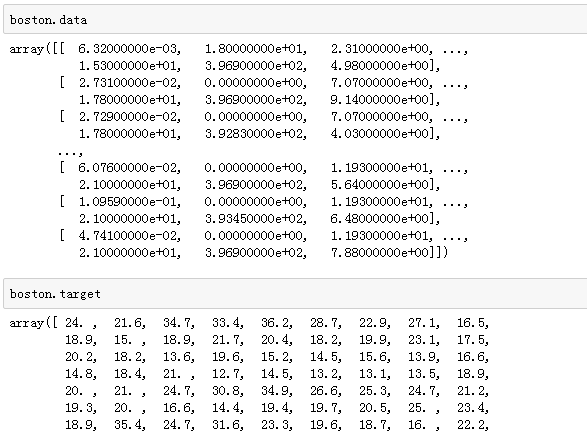
切分数据集

from sklearn.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size = 0.2, random_state=2)

数据预处理

普通的线性回归模型太简单，容易导致欠拟合，我们可以增加特征多项式来让线性回归模型更好地拟合数据。在sklearn中，通过preprocessing模块中的PolynomialFeatures来增加特征多项式。

其重要参数有：

• degree：多项式特征的个数，默认为2
• include_bias：默认为True，包含一个偏置列，也就是 用作线性模型中的截距项，这里选择False，因为在线性回归中，可以设置是否需要截距项。

from sklearn.preprocessing import PolynomialFeaturespoly = PolynomialFeatures(degree=2,include_bias=False)X_train_poly = poly.fit_transform(X_train)X_test_poly = poly.fit_transform(X_test)

模型训练与评估

线性算法使用sklearn.linear_model 模块中的LinearRegression方法。常用的参数如下：

• fit_intercept：默认为True，是否计算截距项。
• normalize：默认为False，是否对数据归一化。

简单线性回归

from sklearn.linear_model import LinearRegressionmodel2 = LinearRegression(normalize=True)model2.fit(X_train, y_train)model2.score(X_test, y_test)# result# 0.77872098747725804

多项式线性回归

model3 = LinearRegression(normalize=True)model3.fit(X_train_poly, y_train)model3.score(X_test_poly, y_test)# result# 0.895848854203947

总结

多项式的个数的不断增加，可以在训练集上有很好的效果，但缺很容易造成过拟合，没法在测试集上有很好的效果，也就是常说的：模型泛化能力差。